 .
.Dies sind die Ergebnisse des 2. OWINF vom 22.04.2006. Wir gratulieren allen Teilnehmern ganz herzlich zu Ihrem Erfolg.
Die ersten 21 Plätze werden Urkunden erhalten und wurden diesbezüglich per Mail kontaktiert. Die Plätze 1, 2 und 4 – also die besten Schüler – wurden mit Büchergutscheinen belohnt.
Wir hoffen, daß allen Teilnehmern Spaß gemacht hat und bedanken uns für Eure Geduld bei den Verzögerungen.
Wie man sehen kann, waren die Aufgaben immer noch sehr schwer – obwohl es natürlich auch gut ist, einen klaren Gewinner zu haben. Vorschläge zur Lösung dieses Problems (wie auch weitere Anregungen und auch Meinungen, z.B. zu "Ich hätte lieber in Java programmiert") nehmen wir immer gerne an, zum Beispiel auf der Mailingliste.
Das OWINF-Team
| Name | manhattan | mobiles | stadt | ∑ |
|---|---|---|---|---|
| Daniel Grunwald |
100
|
50
|
100
|
250 |
| Ludwig Schmidt |
98
|
20
|
100
|
218 |
| Thomas Schneider |
97
|
x
|
100
|
197 |
| Arne Müller |
77
|
x
|
60
|
137 |
| Karsten Behrmann |
62
|
x
|
70
|
132 |
| Julian Fischer |
68
|
x
|
50
|
118 |
| Birtan Özel |
56
|
x
|
30
|
86 |
| Andreas Krüger |
58
|
20
|
x
|
78 |
| Johann Felix von Soden-Fraunhofen |
44
|
x
|
30
|
74 |
| Stefan Toman |
61
|
x
|
10
|
71 |
| N.N. |
69
|
x
|
0
|
69 |
| N.N. |
54
|
10
|
x
|
64 |
| N.N. |
26
|
x
|
30
|
56 |
| N.N. |
55
|
x
|
x
|
55 |
| N.N. |
52
|
x
|
x
|
52 |
| N.N. |
42
|
x
|
x
|
42 |
| N.N. |
41
|
x
|
x
|
41 |
| N.N. |
41
|
0
|
x
|
41 |
| N.N. |
x
|
x
|
40
|
40 |
| N.N. |
x
|
30
|
x
|
30 |
| N.N. |
15
|
0
|
10
|
25 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
Du sollst ein Programm schreiben, dass N Zahlen (1≤N≤500.000) summiert.
Jede dieser Zahlen liegt im Bereich -9.223.372.036.854.775.808 bis 9.223.372.036.854.775.807 – sie paßt also in einen Int64 in Freepascal bzw. einen long long int in g++.
Die Eingabedatei summe.in enthält in der ersten Zeile die Zahl N. Jede weitere Zeile enthält genau eine der zu summierenden Zahlen.
Die erste und einzige Zeile der Datei summe.out soll das Ergebnis enthalten, bzw. ein NEIN, falls das Ergebnis selbst nicht in den Zahlenbereich passt.
Memory: 10 MB
Laufzeit: 2 Sekunden
| summe.in | summe.out |
|
3 4 -2 7 |
9 |
|
2 9223372036854775807 9223372036854775807 |
NEIN |
Hinweis: Im folgenden wird der englische Begriff integer einfach eingedeutscht verwendet. Er bedeutet ganzzahlig oder ganze Zahl. Die Verwendung eines deutschen Äquivalents würde den Text unnötig verkomplizieren. Ebenso wird mit dem Begriff signed bzw. unsigned (vorzeichen-behaftet bzw. nicht vorzeichen-behaftet) verfahren.
Die Lösung der Aufgabe ist technisch relativ schwierig, vor allem da der Umgang mit 64-Bit Integern in C++ zwar inzwischen standardisiert, aber in Lehrbüchern und älteren Compilern Mangelware ist. Daher würde diese Aufgabe wohl nicht im Wettbewerb selbst vorkommen, obwohl es durchaus nützlich sein kann, zu wissen, wie man mit 64-Bit Integern rechnet.
Ein vorzeichenbehafteter 64-Bit Integer kann (in der Zweier-Komplement- Darstellung, die von handelsüblichen Rechnern verwendet wird) genau in dem in der Aufgabe angegebenen Bereich
[-9.223.372.036.854.775.808; 9.223.372.036.854.775.807]
liegen – die Zahlen der Eingabedatei können also in einen solchen eingelesen werden, wie in der Aufgabe angegeben war:
long long a;
scanf("%lld", &a);
bzw.
var a: Int64; begin readln(a);
Jeder Integer-Datentyp hat eine bestimmte Größe: Normalerweise arbeitet man heute mit 32-Bit Integern, da die meisten Prozessoren (wie auch der Auswertungsrechner) mit 32 Bits arbeiten. Sie können aber auch mit 8-, 16- oder 64-Bit Integern umgehen. Im folgenden beziehen sich die Beispiele auf einen 8-Bit Integer – sie gelten aber auch äquivalent für alle anderen Typen.
Zahlen werden im Computer als Bits, d.h. in der Binärdarstellung (oder auch im "Dualsystem") gespeichert:
| Zahl | Binärdarstellung als 8-Bit Integer |
|---|---|
| 0 | 00000000 |
| 1 | 00000001 |
| 2 | 00000010 |
| 3 | 00000011 |
| 4 | 00000100 |
| 5 | 00000101 |
| 100 | 01100100 |
| 127 | 01111111 |
Nun möchte man auch negative Zahlen darstellen können und gibt daher dem ersten Bit die Bedeutung des Vorzeichens.
Anstatt aber die Bedeutung der übrigen Bits einfach gleichzulassen, wie es in der Einer-Komplement-Darstellung der Fall ist
| Zahl | Binärdarstellung als 8-Bit Integer im Einer-Komplement |
|---|---|
| +0=-0 | 10000000 |
| -1 | 10000001 |
| -2 | 10000010 |
| -127 | 11111111 |
(Dies führt zu einigen Problemen, z.B. bei der Addition oder auch durch die zwei Möglichkeiten, die 0 darzustellen, nämlich als 00000000 und als 10000000.), interpretiert man Zahlen i, die eigentlich größer als 127 wären (also genau die, deren erstes Bit gesetzt ist), als i-256:
| Zahl | Binärdarstellung als 8-Bit Integer im Zweier-Komplement | Bedeutung bei Interpretation ohne Vorzeichen |
|---|---|---|
| 0 | 00000000 | 0 |
| -1 | 11111111 | 255 = -1 + 256 |
| -2 | 11111110 | 254 = -2 + 256 |
| -3 | 11111101 | 253 = -3 + 256 |
| -128 | 10000000 | 128 = -128 + 256 |
Interpretiert man das erste Bit als Vorzeichen, so spricht man von einem signed Integer. Interpretiert man alle Bits wie im üblichen Dualsystem ohne Vorzeichen, so spricht man von einem unsigned Integer.
Daher kann ein 8-Bit signed Integer Zahlen im Bereich [-128;127] darstellen (alle hier verwendeten Intervalle schließen ihre Grenzen mit ein), ein 8-Bit unsigned Integer jedoch Zahlen im Bereich [0;255].
Der Vorteil der Zweier-Komplement-Darstellung ist nun, daß signed Integers ohne Probleme "wie in der Schule gelernt" addiert werden können:
| 3 | 00000011 | ||||
| + | (-7) | + | 11111001 | ||
| -4 | 11111100 | ||||
Allerdings kann man bei der Addition sehr leicht aus dem darstellbaren Bereich von [-128;127] herauskommen: Addiert man nämlich zwei zu große Zahlen (etwa 100 und 50) oder zwei zu kleine Zahlen (etwa -120 und -80), so kommt es zu komischen Phenomänen:
| 01100100 | 10001000 | ||||
| + | 00110010 | + | 10110000 | ||
| 10010110 | 1 00111000 | ||||
Das heißt 100+50=-106 und (-120)+(-80)=x?
Ja! Bei der zweiten Rechnung wird das neunte Bit, die führende 1, einfach weggelassen, da sie nicht mehr in den 8 Bits speicherbar ist. Also (-120)+(-80)=56.
Auch wenn diese Rechnungen mathematisch natürlich falsch sind, führt der Computer sie so aus. Man spricht vom Überlauf: Es ist 127+1=-128 und -128-1=127, vorausgesetzt natürlich, daß man mit 8-Bit signed Integern rechnet.
Für größere Zahlbereiche gilt entsprechendes:
| Länge | Bereich des zugehörigen Integer-Typs |
|---|---|
| 8 Bits | signed: -128 bis +127 unsigned: 0 bis +255 |
| 16 Bits | signed: -32,768 bis +32,767 unsigned: 0 bis +65,535 |
| 32 Bits | signed: -2,147,483,648 bis +2,147,483,647 unsigned: 0 bis +4,294,967,295 |
| 64 Bits | signed: -9,223,372,036,854,775,808 bis +9,223,372,036,854,775,807 unsigned: 0 bis +18,446,744,073,709,551,615 |
| 128 Bits | signed: -170,141,183,460,469,231,731,687,303,715,884,105,728 bis +170,141,183,460,469,231,731,687,303,715,884,105,727 unsigned: 0 bis +340,282,366,920,938,463,463,374,607,431,768,211,455 |
| generell: n Bits | signed: -2n-1 bis 2n-1-1 unsigned: 0 bis 2n-1 |
Da auf 32-Bit-Prozessoren nur mit 64-Bit Integern und noch nicht mit 128-Bit Integern gerechnet werden kann, muss man diese Problematik auf jeden Fall berücksichtigen und irgendwie handhaben.
Die im letzten Abschnitt aufgelisteten Informationen kann man nun auf verschiedene Art und Weise verwenden, um das ursprüngliche Problem zu lösen:
So kann man versuchen, den Überlauf komplett zu vermeiden: Man addiert nur Zahlen, bei denen dies ohne Probleme geht, d.h. möglichst zu einer negativen eine positive oder umgekehrt.
Dazu sortiert man zunächst alle Zahlen der Größe nach. Dann summiert man die Zahlen einfach auf, wobei man die nächst kleinste verwendet, wenn die Summe momentan positiv ist, oder die nächst größte, wenn die Summe momentan negativ ist.
Das klappt allerdings nur so lange, wie es tatsächlich nicht zum Überlauf kommt, d.h. die richtige Ausgabe nicht NEIN ist. Tritt bei der Methode ein Überlauf auf, so wäre die richtige NEIN, die in diesem Fall ja auch ausgegeben werden muß. Aber wie entdeckt man, ob das passiert ist?
Nun ja: Hat man zu einer negativen Zahl eine negative addiert und ist das Ergebnis nicht mehr selbst negativ, so ist sicher etwas schiefgegangen – das ist der "Überlauf nach unten". Addiert man entsprechend zu einer positiven Zahl eine weitere positive Zahl und ist dann das Ergebnis negativ, so hat der Überlauf nach oben stattgefunden. In beiden Fällen kann man direkt NEIN ausgeben, da durch die Sortierung so ein Fall nur genau dann auftritt, wenn die endgültige Summe auch außerhalb des Bereiches liegt.
#include <cstdlib>
#include <fstream>
#include <vector>
#include <algorithm>
#include <iterator>
using namespace std;
// C99 defines int64_t in #include <stdint.h>, however, C++ does not
typedef long long int int64_t;
// copy_n is not part of the STL but defined by the commonly used
// SGI STL in #include <ext/algorithm>. For the sake of completeness
// it's repeated here
template <typename InputIterator, typename Size, typename OutputIterator>
pair<InputIterator, OutputIterator>
copy_n(InputIterator first, Size count, OutputIterator result) {
for (; count > 0; count--) {
*result = *first;
++first;
++result;
}
return pair<InputIterator, OutputIterator>(first, result);
}
int main() {
ifstream fin("summe.in");
ofstream fout("summe.out");
std::vector<int64_t> numbers;
int count;
fin >> count;
copy_n(istream_iterator<int64_t>(fin), count,
back_inserter(numbers));
sort(numbers.begin(), numbers.end());
std::vector<int64_t>::iterator begin, end;
begin = numbers.begin();
end = numbers.end();
int64_t sum = 0;
while (begin != end) {
int64_t number = (sum >= 0 ? *begin++ : *--end);
int64_t next_sum = sum + number;
if ((number > 0 ? next_sum < sum : next_sum > sum)) {
fout << "NEIN\n";
return EXIT_SUCCESS;
}
sum = next_sum;
}
fout << sum << "\n";
return EXIT_SUCCESS;
}
Das Programm hat wegen der Sortierung eine Laufzeit von O(N log N) und einen Speicherverbrauch von O(N).
Ein anderer Ansatz geht von folgender Tatsache aus: Läuft das Zwischenergebnis beim Summieren von Zahlen genau so oft "nach oben" über wie "nach unten", so ist die normale Interpretation des Ergebnisses (also genau der Wert) wieder richtig.
Das kann man sich an folgendem 8-Bit-Beispiel klar machen:
(127 + 1) - 1 = 127.
Intuitiv ist das sofort klar. Der Computer jedoch wird zunächst
(127 + 1) - 1 = -128 - 1
rechnen und dann
-128 - 1 = 127.
Das Endergebnis ist genau dann "richtig", wenn die Anzahl der Überläufe nach oben genau die der Überläufe nach unten ist.
Daher zählt man diese einfach mit. Die Erkennung der Überläufe funktioniert genau gleich wie in der ersten Lösung:
#include <cstdlib>
#include <fstream>
using namespace std;
// C99 defines int64_t in #include <stdint.h>, however, C++ does not
typedef long long int int64_t;
int main() {
ifstream fin("summe.in");
ofstream fout("summe.out");
int64_t sum = 0;
int count;
fin >> count;
int overflow = 0, underflow = 0;
while (count--) {
int64_t number;
fin >> number;
int64_t next_sum = sum + number;
if (number > 0 && next_sum < sum)
overflow++;
if (number < 0 && next_sum > sum)
underflow++;
sum = next_sum;
}
if (overflow == underflow)
fout << sum << "\n";
else
fout << "NEIN\n";
return EXIT_SUCCESS;
}
Das Programm hat eine Laufzeit von O(N) und eine Speicherverbrauch von O(1).
Eine weiter Möglichkeit ist die Verwendung von Gleitkommazahlen mit einer Mantisse von mindestens 64 Bits. Allerdings ist es generell bei dem Umgang mit Gleitkommazahlen recht schwierig und trickreich, immer alle Details zu beachten.
Eine Gleitkommazahl f wird im Rechner normalerweise als
f=p m 2e
dargestellt, wobei
| p | das Vorzeichen, also +1 oder -1, darstellt, |
| m | die Mantisse, eine Zahl zwischen 0 und 1, mit einer bestimmten Genauigkeit darstellt, |
| e | der Exponent, ein "normaler" signed Integer ist. |
Die Größe der Mantisse und des Exponenten hängt nun von der verwendeten Architektur und vom Compiler ab. Auf dem Auswertungsrechner liefert ein long double genau eine 64-Bit Mantisse mit einem 15-Bit Exponenten. Zusammen mit dem Vorzeichen (1 Bit) kommt man also auf 80 Bits, also 10 Bytes.
Die 64 Bit der Mantisse mit dem 1-Bit-Vorzeichen erlauben nun die exakte Darstellung von ganzen Zahlen, wie es ein 65-Bit singed Integer tun würde. Die in der Eingabedatei vorkommenden Zahlen lassen sich also alle so darstellen.
Allerdings gibt es noch eine weitere Hürde: Summiert man die Zahlen einfach in der Reihenfolge auf, wie sie in der Eingabedatei vorkommen, so kann es zu Rundungsfehlern kommen (und wird es bei den Testdaten auch): Statt dem Überlauf, wo die führenden Bits verloren gehen, gehen hier einfach die letzten Bits verloren.
Das kann man vermeiden, indem man, sobald die Summe den Bereich [-263;263-1] verläßt, manuell einen Overflow nachprogrammiert und wie in Lösung 2 speichert, wie oft man diesen nach oben bzw. unten durchgeführt hat.
#include <cstdlib>
#include <fstream>
using namespace std;
// C99 defines int64_t in #include <stdint.h>, however, C++ does not
typedef long long int int64_t;
// C99 defines LLONG_MAX and LLONG_MIN in #include <limits.h>
#define LLONG_MAX 9223372036854775807ll
#define LLONG_MIN (-LLONG_MAX - 1ll)
int main()
{
int count;
ifstream fin("summe.in");
ofstream fout("summe.out");
fin >> count;
long double sum = 0.0;
int overflow = 0;
while (count--) {
int64_t value;
fin >> value;
sum += (long double)value;
if (sum > (long double)LLONG_MAX) {
sum -= (long double)LLONG_MAX;
overflow++;
} else if (sum < (long double)LLONG_MIN) {
sum += (long double)LLONG_MAX;
overflow--;
}
}
switch (overflow) {
case -1:
sum -= (long double)LLONG_MAX;
break;
case 1:
sum += (long double)LLONG_MAX;
break;
case 0:
break;
default:
fout << "NEIN\n";
return 0;
}
if (sum > (long double)LLONG_MAX ||
sum < (long double)LLONG_MIN) {
fout << "NEIN\n";
return 0;
}
fout << (int64_t)sum << "\n";
return EXIT_SUCCESS;
}
Nach einer langen Reise durch ganz Amerika ist Elmo endlich wieder in NewYork angekommen. Bevor er wieder nach Europa fliegen wird, möchte er sich noch den schönen Stadtteil Manhattan anschauen. Da er jedoch ein wenig kriminell aussieht, wird er inzwischen von Jack Bauer vom Geheimdienst verfolgt. Der würde gerne Elmo fangen, noch bevor er den Flughafen erreicht. Um seine Fangstrategie zu planen wüsste Jack gerne auf wie vielen Wegen Elmo Manhattan durchqueren kann. Dazu braucht er deine Hilfe.
Dein Programm soll also die folgenden vier Fragen für Jack Bauer beantworten:
| Zeile 1: | n |
| Zeile 2: | m |
| Zeile 1: | Antwort auf Frage 1 |
| Zeile 2: | Antwort auf Frage 2 |
| Zeile 3: | Antwort auf Frage 3 |
| Zeile 4: | Antwort auf Frage 4 |
3
|
5
|
| Laufzeit-Beschränkung: | 1 Sekunde |
| Speicher-Beschränkung: | 32 MB |
Für jede richtige Zahl gibt es 20% der Punkte. Falls ihr alles richtig habt, gibt es nochmals 20%. Damit ihr nicht unter einem Timeout leidet, solltet ihr sobald wie möglich die Zahlen in die Ausgabedatei schreiben und die dann flushen. Dies geht wie folgt:
#include <cstdio>
int main() {
FILE* f = fopen("tim.out", "w");
fprintf(f, "bar\n");
fflush(f);
for (int i = 0; i < 2 ; i=1-i) ;
}
#include <fstream>
using namespace std;
int main() {
ofstream tim("tim.out", ios::out);
tim << "bar\n";
tim.flush();
for (int i = 0; i < 2 ; i=1-i) ;
}
program ti;
var tim:textfile;
i:integer;
begin
assign(tim, 'tim.out');
rewrite(tim);
writeln(tim, 'bar');
flush(tim);
i := 0;
while (i < 3) do
i := 1 - i;
end.
Für jede Frage muss eine Antwort gefunden werden, also beantworten wir die Fragen einfach der Reihe nach:
Mit einer kleinen Skizze kann man recht schnell erkennen, dass Elmo immer n-1 Straßenstücke nach unten und m-1 Straßenstücke nach rechts gehen muss. Die Antwort ist also n+m-2.
Hier wird es etwas komplizierter. Zuerst eine anschauliche Lösung mit dynamischer Programmierung, später dann die deutlich bessere kombinatorische Lösung.
Wenn Elmo an einer Straßenkreuzung ankommt, so kommt er immer von Norden oder von Westen her. Ansonsten wäre er nämlich ein Stück zurück gelaufen und nicht mehr auf dem kürzesten Weg. Die Anzahl der möglichen Wege durch den Straßenknoten (i,j) ist also genau die Summe der Wege durch (i-1,j) plus der Summe der Wege durch (i,j-1). Es gibt nur eine Möglichkeit zu einer Kreuzung am Nord- oder Ostrand zu kommen. Man kann also eine Tabelle aufstellen, in der diese Werte nacheinander berechnet werden. Die Antwort steht am Ende an der Stelle (n-1,m-1) in der Tabelle. Ein Programm, dass diese Tabelle berechnet sieht zum Beispiel so aus:
#include <iostream>
#include <fstream>
using namespace std;
int main() {
int n,m; // Größe von Manhattan
ifstream infile("elmo.in");
infile >> n;
infile >> m;
int table[n][m];
// Anfangswerte:
for(int i=0; i<n; i++) table[i][0] = 1;
for(int i=1; i<m; i++) table[0][i] = 1;
// Rest der Tabelle füllen:
for(int i=1; i<n; i++) {
for(int j=1; j<m; j++) {
table[i][j] = table[i-1][j] + table[i][j-1];
}
}
cout <<"Antwort auf Frage 2: "<< table[n-1][m-1]<<endl;
}
Dieses Programm lässt sich noch ein wenig optimieren, insbesondere der Speicherverbrauch ist quadratisch und könnte durch 'vergessen' der bereits berechneten Werte linear werden. Außerdem ist die berechnete Tabelle symmetrisch, es werden also viele Werte doppelt berechnet.
Eine weit bessere Lösung ist jedoch der folgende kombinatorische Ansatz.
Aus der ersten Antwort wissen wir, dass Elmo n-1 Straßenstücke in südlicher Richtung und m-1 Straßenstücke in östlicher Richtung entlanggeht. Da Manhattan ein vollständiges Gitter (Grid) ist, ist es egal in welcher Reihenfolge er diese Straßenstücke benutzt.
Gesucht ist also die Anzahl der möglichen Anordnungen mit Beachtung der Reihenfolge von insgesamt n+m-2 Dingen, von denen n-1 zu einer Sorte und m-1 zu einer anderen Sorte gehören.
Die Kombinatorik kennt für dieses Problem eine Lösungsformel: (n+m-2)!/((n-1)!*(m-1)!)
Diese könnte direkt implementiert werden, was aber zu Problemen mit größeren Zahlen führt. Ab n+m = 11 würde im Zähler eine Zahl stehen, die zu groß für den 32-Bit Integerbereich ist. Auch die Verwendung von 64-Bit-Zahlen bringt relativ wenig, damit würde man bis n+m = 20 kommen. Die Aufgabenstellung sichert jedoch nur zu, dass das Ergebnis in eine 32-Bit-Zahl passt. Da jedoch auch der Nenner sehr groß werden kann, ist es trotzdem möglich, dass der Zähler nicht mehr in eine 64-Bit-Zahl passt.
Es würde sich also anbieten Funktionen zum Rechnen mit beliebig langen Ganzzahlen zu verwenden. Da solche jedoch leider nicht in jeder Programmiersprache enthalten sind und die Verwendung von externen Bibliotheken beim OWINF nicht erlaubt ist, Werden wir eine andere Lösung suchen.
Die eine Fakultät im Nenner kann sofort mit dem Zähler gekürzt werden. Bei der anderen Fakultät ist das kürzen etwas komplizierter, aber nicht wirklich schwierig. Daher wird der Bruch zuerst vollständig gekürzt und dann die Reste des Zählers multipliziert. So ist sichergestellt, dass nie mit Zahl, die größer als das Ergebnis sind, gerechnet werden muss.
Da wir wissen, dass das Ergebnis eine Ganzzahl ist, lassen sich alle Faktoren des Nenners kürzen. Für jeden Faktor im Nenner kann der größte gemeinsame Teiler mit einem Faktor im Zähler mit dem Euklidischen Algorithmus berechnet werden. Durch diesen werden beide geteilt. Falls ein Rest im Nenner verbleibt, kann dieser mit einem anderen Faktor im Zähler gekürzt werden.
Immer wenn Elmo ein Stück diagonal geht, kommt er ein Stück nach Süden und eines nach Osten weiter. Er spart also eine Minute. Der kürzeste Weg ist also der, der möglichst viele diagonale Wege enthält. Wenn n≥m ist, geht er also diagonal durch m-1 Häuserblöcke. Dann bleiben noch n-m Stücke in östlicher Richtung. Insgesamt also n-1. Im anderen Fall analog m-1.
Diese Frage ist sehr ähnlich zur zweiten und kann auch kombinatorisch gelöst werden. Wieder ist es egal in welcher Reihenfolge die Teilstücke gegangen werden. Wenn n≥m ist, gibt es n-m gerade und m-1 diagonale Straßenstücke. Das macht insgesamt (n-1)!/((n-m)!*(m-1)!) Möglichkeiten, die analog zu Frage 2 berechnet werden.
#include <iostream>
#include <fstream>
using namespace std;
inline int euklid(int, int);
inline int facfrac(int, int, int);
int main()
{
// Eingabe
int n,m; // Größe von Manhattan
ifstream infile("manhattan.in");
infile >> n;
infile >> m;
if(m>n) {
int t = m;
m = n;
n = t;
}
// Ausgabe
ofstream outfile("manhattan.out");
// erste Antwort:
outfile<<m+n-2<<endl;
// zweite Antwort:
outfile<<facfrac(n+m-2, n-1, m-1)<<endl;
// dritte Antwort:
outfile<<n-1<<endl;
// vierte Antwort:
outfile<<facfrac(n-1, n-m, m-1)<<endl;;
// Fertig:
outfile.close();
exit(0);
}
/*
Berechnet x!/(a!*b!)
*/
inline int facfrac(int x, int a, int b)
{
// Alle Faktoren im Zähler berechnen, dabei kann
// a! schon gekürzt werden
int numerator[x-a];
for(int i=(a+1); i<=x; i++)
{
numerator[i-(a+1)] = i;
}
// Die übrigenFaktoren im Zähler
// werdem mit jedem Faktor aus b! gekürzt:
for(int denom=2; denom<=b; denom++)
{
int thisDenom = denom;
for(int num=0; thisDenom>1; num++)
{
if(num == x-a) cout<<"ERROR!!!!!!!!!!!!"<<endl;
// Kürzen mit dem ggT
int gcd = euklid(thisDenom, numerator[num]);
thisDenom/=gcd;
numerator[num]/=gcd;
}
}
// Alle übrigen Faktoren im Zähler miteinander
// multiplizieren:
int res = 1;
for(int i=0; i<(x-a); i++) res*=numerator[i];
return res;
}
/*
Berechnen des größten gemeinsamen
Teilers von a und b mit dem
euklidischen Algorithmus
*/
inline int euklid(int a, int b)
{
while( 1 )
{
a = a % b;
if(a == 0)
return b;
b = b % a;
if(b == 0)
return a;
}
}
Heinrich hat für sein Spielwarengeschäft „Auerbachs Spielkeller“ eine Lieferung Mobiles erhalten. Sie bestehen aus runden Figuren, die durch Schnüre miteinander verbunden sind. Die Lieferung erhält unterschiedliche Typen von Mobiles, die jeweils mit einem oder mehreren Exemplaren vertreten sind. Leider ist die Lieferung unsortiert. Um die Mobiles in seinen Verkaufsräumen anbieten zu können, muss Heinrich sie also erst noch nach gleichen Typen sortieren. Kannst du ein Programm schreiben, dass ihm dabei hilft?
Heinrich hat eine ASCII Darstellung der Mobiles vorbereitet, damit dein Programm sie leichter analysieren kann. Die Figuren stellt er dabei als O (das ist der Buchstabe O, nicht die Zahl 0) dar und die Verbindungsschnüre als waagerechte, senkrechte oder diagonale ASCII Linien durch die Zeichen - (Bindestrich), | (senkrechter Strich), / (slash) und \ (backslash). Dabei gehört ein Bindestrich zu der selben Line, wie der Bindestrich links und der Bindestrich rechts von ihm. Ein senkrechter Strich gehört zur selben Line, wie der senkrechte Strich über und unter ihm. ein Slash Gehört zur selben Linie, wie der slash links unter ihm und der slash rechts über ihm. Beim Backslash verhält es sich analog. Eine Linie „knickt“ niemals ab. Sie besteht immer nur aus einer Sequenz ein und desselben Zeichens. Außerdem endet eine Linie immer in einer Figur (O). Eine Figur gilt nur dann als verbunden mit einer Linie (und damit die Figur als verbunden mit der Schnur), wenn die Linie aus Bindestrichen besteht und von links bzw. von rechts an sie grenzt oder aus senkrechten Strichen besteht und von oben bzw. unten an sie grenzt, etc.
Dies sind korrekte Darstellungen von Mobiles:
O---O O \ / O-O O O | O
Dies sind fehlerhafte Darstellungen von Mobiles:
O / O O-- O-- O/ OO ---
Bei der Überprüfung auf Gleichheit zweier Mobiles, ist die Länge der Schnüre zu ignorieren. Auch sind alle Figuren gleich. Allerdings hat Heinrich die Mobiles so „abgezeichnet“, wie sie im Karton lagen. Zwei gleiche identische Mobiles können also auf den ersten Blick durchaus unterschiedlich aussehen. Die folgenden beiden Mobiles sind beispielsweise identisch:
O---O | / | / |/ O O / \ O---O
Die Eingabedatei mobiles.in enthält die ASCII Darstellungen der gelieferten Mobiles. In der ersten Zeile der Datei steht die Anzahl 1 ≤ n ≤ 1000 der gelieferten Mobiles. In der zweiten Zeile stehen 1 ≤ w, h ≤ 30.
Es folgen n Blöcke von jeweils h Zeilen Länge, die jeweils w Zeichen breit sind (plus das anschließende Newline Zeichen). Jeder dieser Blöcke enthält die ASCII Repräsentation eines der gelieferten Mobiles. Er besteht also ausschließlich aus den Zeichen - | / \ und dem Leerzeichen (plus die Newlines am Zeilenende). Beachte: Jede Zeile ist exakt w Zeichen lang. Gegebenenfalls sind die Zeilen mit Leerzeichen aufgefüllt oder bestehen gänzlich aus Leerzeichen.
Es wird garantiert, dass nie mehr als 20 Figuren am Mobile hängen.
Schreibe in die erste Zeile der Datei mobiles.out die Anzahl m von unterschiedlichen Mobile-Typen, die du gefunden hast. Für jeden der m Typen soll eine Zeile folgen, die durch Leerzeichen separiert die Nummer der Eingabe-Blöcke enthält, die ein Mobile vom jeweiligen Typ beschrieben haben.
Memory: 10 MB
Laufzeit: 1 Sekunde
| mobiles.in | mobiles.out |
| 3 5 5 O---O | / | / |/ O O / \ O---O O-O-O |
2 1 2 3 |
Bei diesem Problem handelt es sich "einfach" um das der Graphen-Isomorphie.
Zwei Graphen (bestehend aus Knoten und Kanten) heißen isomorph, wenn es eine Eins-zu-Eins-Zuordnung zwischen ihren Knoten und Kanten gibt, so daß entsprechende Kanten genau ihre entsprechenden Knoten verbinden. Anders formuliert: Wenn die beiden Mobiles wie in der Aufgabe beschrieben genau "gleich" sind.
Die Komplexität des Tests auf Graphen-Isomorphie ist unbekannt, es wird im allgemeinen zwischen P und NP angesiedelt. Der übliche Ansatz ist ein optimiertes Backtracking über alle möglichen Eins-zu-Eins-Zuordnungen der Knoten, von denen es bei N Knoten N! gibt.
Isomorphe Graphen bilden eine Klasse (da die Isomorphie eine Äquivalenzrelation darstellt - was hier zu weit führen würde), d.h. man kann sie in Mengen einteilen, bei denen jeder Vertreter aus ihnen jeweils repräsentativ für die gesamte Menge ist. Grob gesagt tut man gleiche Graphen zu gleichen.
Man erstellt zunächst eine Funktion, die testet, ob zwei Graphen gleich sind. Dann liest man die Graphen Stück für Stück ein und klassifiziert sie: Paßt der aktuell eingelese Graph zu einer bereits vorhandenen Klasse (d.h. ist er "gleich" einem beliebigen Vertreter aus dieser Klasse), so fügt man ihn zu der Klasse hinzu. Paßt er nirgends dazu, so macht man für ihn eine neue Klasse auf, deren einziger Vertreter er (bisher) ist.
Am Ende gibt man für jede Klasse die Nummern ihrer Graphen (=die Positionen in der Eingabedatei) jeweils zeilenweise aus.
Schon das Einlesen der Daten ist bei diesem Problem nicht gerade einfach. Die Beispiellösung, die unten zu sehen
ist, tut dies (nachdem ein einzelnes Mobile in einen char Array eingelesen wurde) in zwei Schritten:
Zunächst wird festgestellt, welche Knoten es überhaupt gibt. Diese werden
dann in eine map, nämlich nodes gespeichert. Eine map funktioniert
ähnlich wie ein Wörterbuch: auf Anfrage kann man einen Wert zu einem bestimmten "Schlüssel"
erhalten. Als Schlüssel werden in diesem Fall die Koordinaten des Knotens verwendet, und zwar in Form von
einem pair<int,int>, oder kurz PII, wie es hier benannt ist. Jedem Knoten
wird eine eindeutige Zahl zugeordnet. Unter dieser Zahl kann man den Knoten später im Mobile-Array wiederfinden.
Dieser Schritt ist in der for-Schleife nach "MPIII nodes;" zu sehen.
Im zweiten Schritt werden dann nocheinmal alle Knoten in der Eingabe angeschaut. Diesesmal wird untersucht, ob sich
Verbindungsstücke in einem der acht benachbarten Felder befinden. Sollte sich beispielsweise unter dem Knoten
PII(y,x) das Zeichen '|' befinden, so ist klar, dass dieser Knoten mit einem anderen Knoten
PII(y+dy,x) verbunden sein muss: und zwar mit demjenigen, für den dy möglichst
klein ist. Die Funktion graph_add sucht genau diesen Knoten. Damit die Funktion für
Verbindungen in anderen Richtungen wiederverwendet werden kann, erhält sie als Parameter die Werte dy
und dx, die jeweils 1, 0, oder -1 sein können und die
Richtung angeben, in der der verbundene Knoten gesucht wird.
Der letzte Parameter der Funktion graph_add heißt mob und ist eine Referenz
auf das entsprechende Mobile. Ein Knoten im Mobile ist ein vector, also ein Array, von ints:
nämlich die Indizes der verbundenen Knoten. Ein neu gefundener Knoten wird dieser Liste hinzugefügt.
Entsprechend besteht ein Mobile aus einem vector<vector<int> >,
kurz VVI. Nachdem eine komplette Datei eingelesen worden ist, beinhaltet mobiles einen
vector von Mobiles, genau in dem oben beschriebenen Format.
Nachdem alle Mobiles in einem brauchbaren Format vorliegen, muss festgestellt werden, wieviele verschiedene
Arten von Mobiles es gibt (d.h. wieviele Äquivalenzklassen). Der vector classes
ist zunächst leer: er soll letztendlich einen Eintrag pro Mobileart enthalten. Das Prinzip ist recht
einfach: Jedes Mobile wird mit jeder bisher gefundenen Art von Mobiles verglichen und falls ein Mobile
zu keinem anderen gleich ist, wird es als neue Mobileart zu classes hinzugefügt.
Das Problem stellt dabei das überprüfen auf Gleichheit dar. Dieser Test wird von der Funktion
isomorph vorgenommen (sie ruft traverse als Hilfsfunktion auf). Zunächst
kann man natürlich ein paar triviale Dinge überprüfen: Ist die Anzahl der Knoten in
beiden Graphen gleich? Hat jeder Graph gleichviele Knoten mit gleichem Grad (d.h. mit gleichvielen
Verbindungen)? Erst wenn beide Bedingungen erfüllt sind, wird der Test kompliziert: gesucht ist
eine Zuordnung jedes Knotens in a zu seinem "Partner" in b.
Leider müssen dazu (fast) alle Zuordnungen durchprobiert werden, bis eine passende gefunden ist.
Die Variable asgn[i] beinhaltet den Index von Graph b, der aktuell zum Knoten mit
dem Index i in Graph a zugeordnet ist. Die for-Schleife in
isomorph probiert alle möglichen Werte für asgn[0] durch und
übergibt den Rest der Arbeit an die Funktion traverse. Diese Funktion findet noch
nicht zugeordnete Knoten und ordnet diese zu, bis sich ein Widerspruch ergibt, oder die Zuordnung
vollständig ist. Ein Widerspruch ergibt sich genau dann, wenn in Graph a
Knoten i mit Knoten j verbunden ist, aber es im Knoten asgn[i] im
Graph b keine Verbindung zu Knoten asgn[j] gibt. In diesem Fall
gibt die Funktion 0 zurück und die nächste Zuordnung wird durchprobiert,
bis es keine Widersprüche gibt, oder alle Zuordnungen probiert worden sind. Es ist übrigens
wesentlich einfacher, diese Funktion selber zu implementieren (wenn sie
verstanden worden ist), als ihren Quelltext zu dechiffrieren.
#include <cstdio>
#include <vector>
#include <map>
using namespace std;
FILE *fin=fopen("mobiles.in","r"),
*fout=fopen("mobiles.out","w");
int M;
typedef vector<int> VI;
typedef vector<VI> VVI;
typedef vector<VVI> VVVI;
typedef pair<int,int> PII;
typedef map<PII,int> MPIII;
VVVI classes;
VVVI mobiles;
int W, H;
// verbundenen Knoten suchen
int graph_add(int x, int y, int dx, int dy, MPIII &nodes, VVI &mob){
int cx=x+dx,cy=y+dy;
while(true){
if(nodes.find(PII(cy,cx))!=nodes.end()){
mob[nodes[PII(y,x)]].push_back(nodes[PII(cy,cx)]);
return 0;
}
cx+=dx;cy+=dy;
}
return 0;
}
// Verschiedene Knotenzuordnungen durchprobieren
// a und b sind die beiden Graphen
// na und nb beinhalten zwei Knoten, die einanderzugeordnet sind
// used speichert, welche Knoten von b schon zugeordnet sind
// asgn[i] speichert, welchem Knoten in b, der Knoten i in a zugeordnet ist
int traverse(VVI &a, VVI &b, int na, int nb, int i, VI &asgn, int used){
// Grad der beiden aktuellen Knoten vergleichen
if(a[na].size()!=b[nb].size()) return 0;
// Sind alle Knoten zugeordnet
if(i==a[na].size()) return 1;
int ok=1;
for(int k=0;k<a.size();k++)
if(((used>>k)&1)==0)ok=0;
if(ok) return 1;
// Ist die aktuelle Verbindung schon zugeordnet
if(asgn[a[na][i]]!=-1){
// Ja: gucken, ob die Zuordnung konsistent ist
int f=0;
for(int j=0;j<b[nb].size();j++){
if(b[nb][j]==asgn[a[na][i]]){
f=1;
break;
}
}
if(!f) return 0;
traverse(a,b,na,nb,i+1,asgn,used);
} else {
// Nein: alle moeglichen Zuordnungen durchprobieren
for(int j=0;j<b[nb].size();j++){
if(((used>>b[nb][j])&1)==0){
asgn[a[na][i]]=b[nb][j];
if (traverse(a,b,a[na][i],b[nb][j],0 ,asgn,used|(1<<b[nb][j])) &&
traverse(a,b,na ,nb ,i+1,asgn,used|(1<<b[nb][j]))){
asgn[a[na][i]]=-1;
return 1;
}
asgn[a[na][i]]=-1;
}
}
return 0;
}
}
// Stellt die Gleichheit zweier Graphen fest.
int isomorph(VVI &a, VVI &b){
// Unterschiedliche Anzahl von Knoten: Graphen können nicht gleich sein.
if(a.size()!=b.size()) return 0;
// Anzahl der Knoten mit verschiedenen Graden zaehlen
VI aedges(20,0),bedges(20,0);
for(int ia=0;ia<a.size();ia++){
aedges[a[ia].size()]++;
bedges[b[ia].size()]++;
}
// Vergleichen, ob Anzahlen uebereinstimmen
for(int i=0;i<aedges.size();i++)
if(aedges[i]!=bedges[i])return 0;
// Alle moeglichen Knotenzuordnungen durchprobieren
for(int bi=0;bi<b.size();bi++){
VI asgn(a.size(),-1);
asgn[0]=bi;
if(traverse(a,b,0,bi,0,asgn,(1<<bi)))
return 1;
}
return 0;
}
int main(){
fscanf(fin,"%d %d %d",&M,&W,&H);
char tmp;
fscanf(fin,"%c",&tmp);
for(int m=0;m<M;m++){
char lines[32][32];
// Ganzes Mobile in char-Array einlesen
for (int h=0;h<H;h++)
fgets(lines[h],32,fin);
MPIII nodes;
// Schritt 1: Knoten finden und Indizes zuordnen
for(int w=0;w<W;w++){
for(int h=0;h<H;h++){
if(lines[h][w]=='O'){
int t=(int)nodes.size();
nodes[PII(h,w)]=t;
}
}
}
VVI mob(nodes.size());
// Schritt 2: Knoten verbinden
for(int w=0;w<W;w++){
for(int h=0;h<H;h++){
if(lines[h][w]=='O'){
if(h<H-1&& lines[h+1][w ]=='|') graph_add(w,h, 0, 1,nodes,mob);
if(h>0 && lines[h-1][w ]=='|') graph_add(w,h, 0,-1,nodes,mob);
if(w<W-1&& lines[ h][w+1]=='-') graph_add(w,h, 1, 0,nodes,mob);
if(w>0 && lines[ h][w-1]=='-') graph_add(w,h,-1, 0,nodes,mob);
if(h>0 &&w>0 &&lines[h-1][w-1]=='\\') graph_add(w,h,-1,-1,nodes,mob);
if(h<H-1&&w>0 &&lines[h+1][w-1]=='/') graph_add(w,h,-1,+1,nodes,mob);
if(h<H-1&&w<W-1&&lines[h+1][w+1]=='\\') graph_add(w,h,+1,+1,nodes,mob);
if(h>0 &&w<W-1&&lines[h-1][w+1]=='/') graph_add(w,h,+1,-1,nodes,mob);
}
}
}
// Mobile abspeichern
mobiles.push_back(mob);
}
// Verschiedene Klassen finden
VVI class_graphs;
for(size_t v=0;v<mobiles.size();v++){
int f=0;
for(size_t c=0;c<classes.size();c++){
if(isomorph(mobiles[v],classes[c])) {
// speichern, dass dieser Graph zur Klasse c gehoert
class_graphs[c].push_back(v+1);
f=1;
break;
}
}
if(!f){
class_graphs.push_back(VI());
class_graphs.back().push_back(v+1);
// speichern, dass dieser Graph zur neuen Klasse gehoert
classes.push_back(mobiles[v]);
}
}
// Ausgabe
fprintf(fout,"%d\n",(int)classes.size());
for(int c=0;c<classes.size();c++){
fprintf(fout,"%d",class_graphs[c][0]);
for(int d=1;d<class_graphs[c].size();d++){
fprintf(fout," %d",class_graphs[c][d]);
}
fprintf(fout,"\n");
}
}
In Süd-Berlin soll ein neues Stadtviertel entstehen. Im Gegensatz zu normalen Stadtvierteln soll dieses neue Stadtviertel jedoch von vorne bis hinten druchgeplant werden, damit ein vollständiges und konsistentes Design entsteht, um Süd-Berlin zu repräsentieren.
Unter anderem müssen auch die Glasfaserkabel für die Standleitungen, die serienmäßig in jeder Wohnung vorzufinden sind, verlegt werden. Nun ist es allerdings so, dass eine Glasfaserleitung nicht nur von einem Haus verwendet wird, sondern direkt zu anderen Häusern weiterverlegt werden kann. Da natürlich die finanziellen Mittel knapp sind, wird nun ein Netzwerk gesucht, welches alle Häuser irgendwie (evtl. indirekt) miteinander verbindet, und dabei so wenig Glasfaserkabel wie möglich verwendet. Die Koordinaten aller geplanten Häuser sind bekannt und liegen als ganzzahlige Werte zwischen 0 und 1000 (inklusive) vor. Die Leitungen können auf jeden Fall auf direktem Weg zwischen jedem beliebigen Häuserpaar verlegt werden und alle Verbindungen sind bidirektional.
Nun wurde Elmo beauftragt, ein entsprechendes Netzwerk zu finden. Leider hat er jedoch einen wichtigen Fernsehauftritt bei Viva und deshalb musst du ihm helfen! Schreibe ein Programm, welches die Koordinaten von bis zu 1000 Häusern einliest und ein Netzwerk ausgibt, welches so wenig Glasfaserkabel wie möglich verbraucht, ausgibt.
| Zeile 1: | N, die Anzahl der geplanten Häuser im neuen Stadtviertel (1 ≤ N ≤ 1000). |
| Zeile 2 + j (0 ≤ j ≤ N - 1): | Zwei ganze Zahlen x, y, die Koordinaten des j-ten Hauses (0 ≤ x, y ≤ 1000). |
| Zeile 1: | K, die Summe der Länge aller verwendeten Glasfaserkabel, auf zwei Dezimalstellen genau gerundet. |
| Ab Zeile 2: | r, s, Die beschreibung des Netzwerks in Form von Kanten, wobei "r, s" eine Verbindung von Haus r nach s und umgekehrt bedeutet. |
5
|
8.00
|
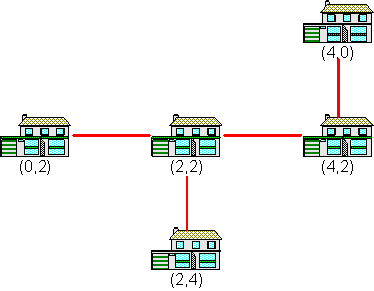
Jede der Verbindungen hat eine Länge von 2.00 Längeneinheiten. Da es vier Verbindungen gibt, werden insgesamt 8.00 Längeneinheiten Glasfaserkabel benötigt.
| Laufzeit-Beschränkung: | 2 Sekunden |
| Speicher-Beschränkung: | 32 MB |
Für diese Aufgabe ist es besonders wichtig, dass man erkennt, dass das Stadtviertel
einen Graphen darstellt: Die Häuser sind die Knoten und es gibt Kanten zwischen
jeweils zwei verschiedenen Häusern (mit einer Kantenlänge, die der Entfernung beider
Häuser entspricht). Auch das Ergebnis ist natürlich nichts anderes als ein Graph.
Die erste Beobachtung, die man machen kann, ist, dass der Graph des Ergebnisses
keine Zyklen haben darf und natürlich zusammenhängend sein muss: Angenommen es gäbe
einen Zyklus im Ergebnis, dann könnte man einfach seine teuerste Verbindung löschen
und jedes Haus häte immer noch Internetanschluss, aber das Netzwerk ließe sich mit
weniger Glasfaserkabel realisieren. Das bedeutet, dass das Ergebnis für ein Stadtviertel
mit N Häusern ein Graph mit genau N-1 Kanten ist. Weiterhin ist
die Lösung ein Baum, und zwar ein sogenannter minimaler Spannbaum (engl: minimum
spanning tree, kurz MST). Der bekannteste Algorithmus zur Berechnung eines minimalen
Spannbaumes ist der Algorithmus von Kruskal und Prim (siehe T.H. Cormen, "Introduction
to Algorithms, Second Edition", S. 567ff.). Er hat eine Laufzeitkomplexität proportional
zu E lg V, in diesem Fall also V2 lg V. Obwohl diese
Laufzeitkomplexität locker ausreicht und die meisten anderen Algorithmen zu aufwendig
zu implementieren sind, sei an dieser Stelle auf den
schnellsten bekannten
Algorithmus von Bernard Chazelle (O(E α(E,V)), α ist
die inverse Ackermannfunktion) hingewiesen.
Im Prinzip geht der Algorithmus wie folgt vor: Man geht davon aus, dass man bereits einen minimalen Spannbaum besitzt. Zunächst besteht dieser einfach nur aus einem Haus ohne jegliche Kanten. Nun ist es so, dass die kürzeste Kante, die von diesem Knoten ausgeht, auf jeden Fall zum minimalen Spannbaum gehören muss. Diese Kante ist nämlich dafür verantwortlich, diesen Knoten mit dem Rest vom Netzwerk zu verbinden. Wenn es also eine kürzere Kante gäbe, würde man stattdessen diese benutzen. Damit hat man bereits einen weiteren Knoten gefunden, der zum Netzwerk gehört. Auf dieselbe Art und weise fährt man nun fort: man sucht immer die kürzeste Kante, die das den bestehenden minimalen Stammbaum zu irgendeinem Knoten verbindet, der sich nicht im Baum befindet. Dann fügt man diesen Knoten und diese Kante hinzu, bis kein Knoten mehr übrig ist.
#include <cstdio>
#include <vector>
#include <set>
#include <list>
#include <cmath>
using namespace std;
FILE *fin=fopen("stadt.in","r"),
*fout=fopen("stadt.out","w");
typedef pair<int,int> PII;
typedef vector<PII> VPII;
typedef vector<int> VI;
typedef vector<VI> VVI;
typedef set<int> SI;
typedef list<PII> LPI;
typedef long double LD;
VPII coords;
VVI dist;
VI startpoint;
LPI edges;
int N;
LD totdist=0.0;
// Quadrat des Abstandes zwischen zwei Haeusern
int getdist(int a,int b){
int x=(coords[a].first-coords[b].first),
y=(coords[a].second-coords[b].second);
return x*x+y*y;
}
int main(){
fscanf(fin,"%d",&N);
coords=VPII(N);
for(int n=0;n<N;n++){
fscanf(fin,"%d %d",&coords[n].first,
&coords[n].second);
}
// Abstandsmatrix fuellen
dist=VVI(N,VI(N,0));
for(int a=0;a<N;a++)
for(int b=a;b<N;b++)
dist[a][b]=dist[b][a]=getdist(a,b);
startpoint=VI(N,0);
// Gruppen anlegen
SI groups;
for(int n=1;n<N;n++)groups.insert(n);
// Gruppen zusammenfuehren
for(int n=1;n<N;n++){
int minb=-1,mind=-1;
// Haus mit minimalem Abstand finden
for(SI::iterator it=groups.begin();it!=groups.end();it++){
int cd=dist[0][*it];
if(mind==-1||mind>cd){
mind=cd;
minb=*it;
}
}
totdist+=sqrt((LD)mind);
// Haus entfernen
groups.erase(minb);
// Kante speichern
edges.push_back(PII(startpoint[minb],minb));
// Abstaende aktualisieren
for(SI::iterator it=groups.begin();it!=groups.end();it++){
if(dist[0][*it]>dist[minb][*it]){
dist[0][*it]=dist[minb][*it];
startpoint[*it]=minb;
}
}
}
// Ausgabe
fprintf(fout,"%.2Lf\n",floor(totdist*100+0.5)/100.0);
for(LPI::iterator it=edges.begin();it!=edges.end();it++)
fprintf(fout,"%d %d\n",it->first,it->second);
return 0;
}
Um später Zeit zu sparen, wird das Quadrat der Abstände direkt nach dem Einlesen
berechnet und in der Variablen dist abgespeichert. Es ist sinnvoll, das Quadrat
zu berechnen, da dann keine Floatingpoint-Zahlen benutzt werden müssen und Rundungsfehler
vermieden werden. Das set groups speichert, welche Knoten des
Graphen noch nicht zum minimalen Spannbaum gehören. Am Anfang sind das alle Knoten,
außer dem mit dem Index 0, denn mit diesem wird der Baum begonnen. Der
Hauptteil des Algorithmus findet sich in der großen for-Schleife und besteht daraus,
dass aus dem set der Knoten mit dem geringsten Abstand gesucht wird. Ist dieser
gefunden, so wird er zunächst aus dem set entfernt. Dann müssen allerdings noch
die Abstände aller Knoten, die noch nicht im Baum sind, aktualisiert werden: dist[0]
wird nämlich verwendet, um den kürzesten Abstand eines Knotens zum Baum zu speichern
und nicht zu Knoten 0. Damit trotzdem nicht die Information verloren geht, von welchem
Knoten aus genau diese kürzeste Verbindung zustande gekomme ist, wird in startpoint
der Anfangspunkt der Kante gespeichert.